今回はデータ同化と呼ばれる技術をご紹介したいと思います🐜
この技術は、新卒で入社した会社で退職するきっかけにもなったもので、すごく思い出深い技術です(白目)
本記事では概念を理解してもらうために、できるだけ数学的議論は省くため、厳密には間違いがあるかもしれません。
ご容赦いただけると幸いです。
データ同化
ざっくりと解説します。
ざっくり解説
昨今AI(人工知能)なるものが流行っていますが、みなさんはどういったものを想像するのでしょうか?
きっとターミネータみたいな世界を想像されるかもしれませんが、実際の現場は結構泥臭いですw
機械学習(AIという言葉好きでないので、こちらの言葉で以下進めます)では、とにかくデータが必要です。
このデータを集めるのが想像以上に難しい。ちなみに、ここでいうデータとは「きちんと機械学習に使える」「意味のあるデータ」を指します。
成果が出ない機械学習をテーマとしたプロジェクトの殆どが、
- 機械学習できるだけのデータ量がそもそもない
- データ形式がぐっちゃぐちゃで前処理に膨大な工数がかかり、分析にたどり着かない
- 因果関係のあるデータセットではない
- ただ流行りのAIでサービスや製品を作ることが目的になっている(←論外だが、これが珍しい話ではない)
といった課題を抱えています。
少し脱線しましたが、これらの課題をクリアしたとしても、なかなか成果が挙げられないのが現状です。
そこで、もしあなたが時系列データの解析を担当する方なら、こう一度は考えたはずです。
自分が今作ろうとしている機械学習モデルを他所から持ってきて、いい感じでデータに馴染ませて、新しいモデルを生成して、いい感じに予測とかできちゃったりしないかなぁ
データ同化とはまさにそれを実現するもので、「先人たちが作り上げてきたモデルを、観測値に同化させて新たなモデルとする」技術です。
もうちょい専門的なざっくり解説
どんなに素晴らしいモデルでも、予測値には必ず誤差が生じ、あくまでも近似値です。同じように、どんなに高性能なセンサを使っても、その値(観測値)には必ず誤差が生じます。
データ同化は、それぞれに生じてしまう誤差を確率分布で表現することで許容し、モデルの予測値とセンサの観測値の間にある、「真値」をうまく推定してやろうという技術です。
難しい表現をしていますが、データ同化の具体的な技術としては、カルマンフィルタや粒子フィルタが挙げられ、よくロボットの自己位置推定(SLAM)や気象予報1などで応用されています。
特にカルマンフィルタはアポロ計画で使われたことが一番有名ですね。
なお、これは長所であり短所でもありますが、データ同化においてモデルがあることが必須です。
データ同化の概念を表現した図を以下に示します。
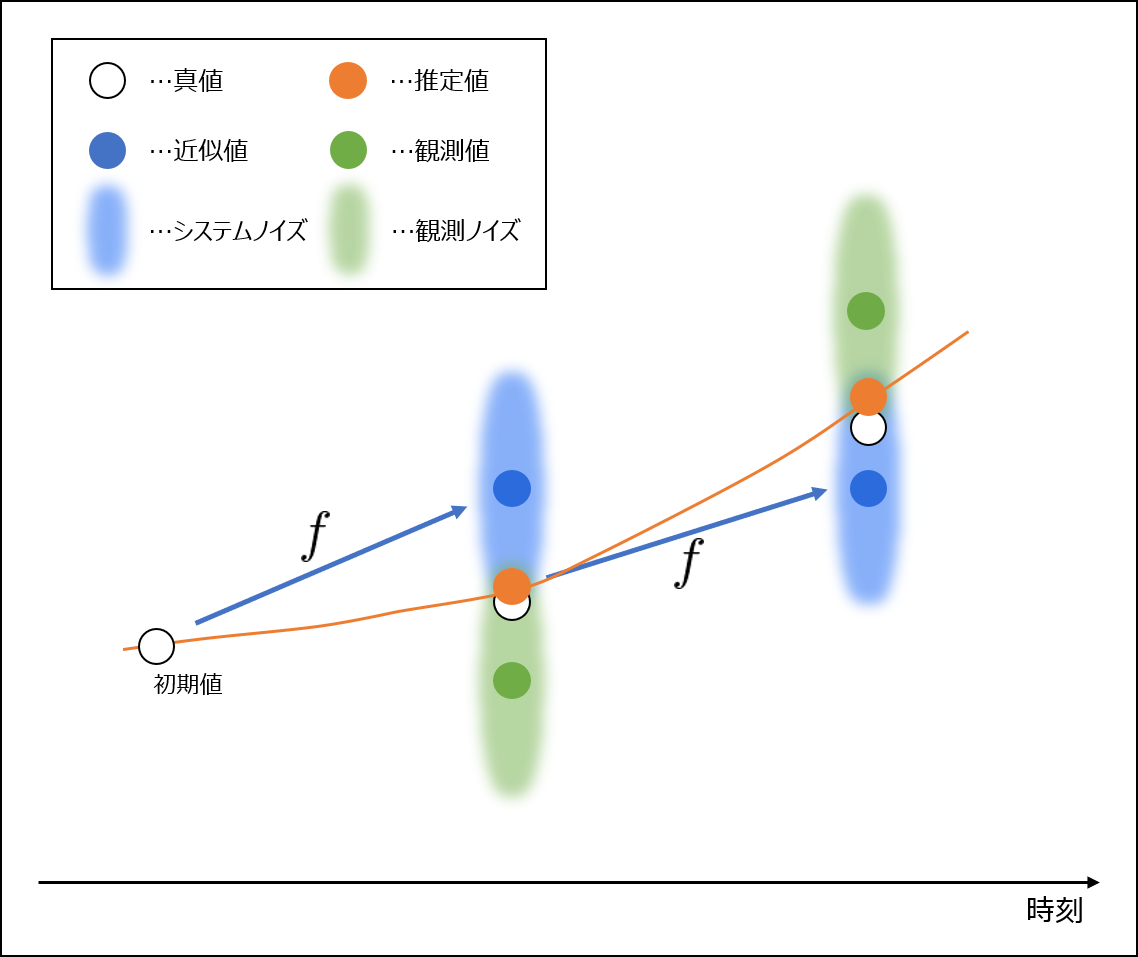
データ同化では、(シミュレーション)モデルから計算する近似値と、センサなどで得た観測値の間にある、数学的または確率的に真値に近い値を推定しながら、時刻を進めます。モデルが観測値に馴染むようなイメージを持っていただければOKです。
ちなみに、データ同化はベイズ統計学またはベイズの定理から発展した技術であるので、ベイズ推定やベイズ機械学習とほぼ同じものです(少なくとも私は同じものだと捉えています)。2
状態空間モデル
データ同化では、まず対象となる系の状態空間モデルを構築します。状態空間モデルは、システムモデルと観測モデルの2つから表現するモデルです。
システムモデル
今、時刻の値
から次の時刻
の値
を求めたいとする。
から
に時間発展する関係式を関数
とすると、以下で表せる。
ここでは以降の説明のため、関数をシミュレーションモデルと呼ぶ。
さて、もしこのがすべての現象を表現できる完璧なシミュレーションモデルであるならば、
は真値となり、以下のように書き直すことができる。
しかし、残念ながらが存在することはなく、シミュレーションモデルで求められる値はあくまでも近似値
である。
真値と近似値
の間には間違いなく差分があり、それを
とすると最初に出した式は以下のように書き直すことができる。
上記の式をシステムモデルと呼び、をシステムノイズと呼ぶ。このシステムモデルは、シミュレーションモデルの持つ誤差をシステムノイズ
を使って表現し、曖昧さを許容した数式である。
なお、このシステムノイズは時刻のある定められた値ではなく、モデルに応じた確率分布に従う値を取ることに注意する。これを式で表すと次のようになる。
観測モデル
今度は、時刻の値
を観測したときの観測値を
とする。ここでの「観測」とは、例えばセンサを使って、ある物理量を測定することとしてもよい。
システムモデルのときと同じように、完全なセンサは存在しないため、やはり真値であると観測値
の間には必ず差分がある。
を真値
と観測値
の差分(または誤差)、
を真値
と観測値
の関係を表す関数とすると、以下のように書ける。
上記の式を観測モデルと呼び、を観測ノイズと呼ぶ。
なお、システムノイズと同様に観測モデルも、モデルに応じた確率分布に従う値を取るので、以下のように書ける。
観測ノイズ
ところで、一見観測ノイズは測定誤差であるように見えるが、それは間違いである。なぜなら、もし観測ノイズが測定誤差と一致するのであれば、このモデル式がセンサ周りの自然現象を完璧に表現できることになってしまい、現実にはありえない再現性を有していることになってしまう。
したがって、観測ノイズは測定誤差以外の表現誤差を含めて設定する必要がある。言い換えれば、観測ノイズ=測定誤差+表現誤差とも言える。
状態空間モデルの実際
改めて、システムモデルと観測モデルを以下に書く。
上記の2つの式を合わせて状態空間モデルと呼ぶ。データ同化を使うときにはまずこの状態空間モデルを構築するところから入る。
初期値の設定の仕方
本来であれば、初期値は真値である必要がありますが、現実には知ることのできない値です。
系にもよりますが、毎回必ず同じ初期値であればあらかじめ決めてしまうか、観測値をそのまま入れてしまうかのどちらかだと思います。
一方でデータ同化技術の特徴として、シミュレーション(正しくはAssimilation)を回すと観測値にモデルが馴染んでいくので、極端に外れた値でなければ条件次第では問題ないとも言えます。
システムノイズの設定の仕方
システムノイズは、平均ゼロの正規分布に従うと仮定すると考えるのがほとんどだと思います。
問題は分散の値ですが、尤度を使って合わせていくのが現実だと思います。ここがある意味、データ同化を扱う難しさとも言えます。
なお、分散を
→そんなことありませんね。カルマンフィルタや粒子フィルタなど処理を進めていくと、ノイズは時間変化していきます。と表現していますが、時刻
によらず一定値とみなすがほとんどです。
観測ノイズの設定の仕方
観測ノイズは、システムノイズと同様に平均ゼロの正規分布に従うと仮定するのがほとんどです。
分散は、もしセンサを使っているのであれば、センサの仕様からチューニングします。
なお、分散を
→そんなことありませんね。カルマンフィルタや粒子フィルタなど処理を進めていくと、ノイズは時間変化していきます。と表現していますが、システムノイズと同様に時刻
によらず一定値とみなすがほとんどです。
おわりに
データ同化の概念をざっくりまとめました。
私が最初にこの技術に触れたときは、結構感動したんですが、それが少しでも伝わればいいなと思います。
参考になれば幸いです(^^)
なお、データ同化関連の記事は以下にあります。よろしければ、こちらもご覧ください。
Data assimilation カテゴリーの記事一覧 - ari23の研究ノート
参考文献
参考文献は以下の通りです。
データ同化入門 (予測と発見の科学)
データ同化分野で私にとってのバイブルです。決して簡単ではないですが、数学的議論がかなりきちんとなされています。データ同化に取り組むときは、まずこれを読んでいます。データ同化―観測・実験とモデルを融合するイノベーション
上記の『データ同化入門』を読んだあとの、補足的な読み物としては良いと思います。でも、この技術書から入門するのはちょっととっつきにくいかも。予測にいかす統計モデリングの基本―ベイズ統計入門から応用まで (KS理工学専門書)
平易な文章で解説されていますので、かなり実装の手助けになると思います。