今回のテーマはディジタル信号処理です🐜
その中でも、周波数解析またはFFTの要点について整理したいと思います。1
もちろん、継続的に加筆修正していきます!
- 周波数解析
- フーリエ変換|連続時間領域と連続周波数領域
- 離散時間フーリエ変換|離散時間領域と連続周波数領域
- 離散フーリエ変換|離散時間領域と離散周波数領域
- 高速フーリエ変換(FFT)
- フーリエ変換のまとめ
- 実装時のポイント
- 付録|複素数 オイラーの公式
- おわりに
- 参考文献
周波数解析
周波数解析(スペクトル解析)とは、信号にどんな周波数の周期信号が含まれているのかを解析することである。
信号にフーリエ変換を施して、時間領域から周波数領域に変換して解析する。
フーリエ変換|連続時間領域と連続周波数領域
フーリエ変換は、信号を連続時間領域→連続周波数領域に変換する。 もちろん、フーリエ逆変換または逆フーリエ変換は、信号を連続周波数領域→連続時間領域に変換する。
フーリエ変換の定義式を以下に示す。
フーリエ逆変換の定義式を以下に示す。
ただし、を周期、
を周波数としたとき、
が成り立つ。
この
は(非正規化)角周波数を表す連続変数であり、
)は
に含まれる角周波数
の振動成分の量を示す。
ちなみに、
は
の振幅スペクトル、
は
の位相スペクトル、
は
のパワースペクトルと呼ぶ。
これを線形・時不変システムで図示すると以下の通り。
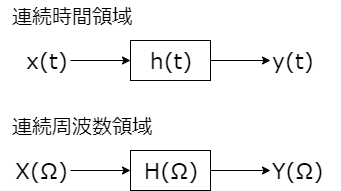
なお、畳み込み式は次式で定義される。
しかし、計算機(ディジタルな領域)で解析するには、離散化が必要であることがわかる。
離散時間フーリエ変換|離散時間領域と連続周波数領域
離散時間フーリエ変換(Dicrete-Time Fourier Transform; DTFT)は、信号を離散時間領域→連続周波数領域に変換する。 もちろん、離散時間フーリエ逆変換は、信号を連続周波数領域→離散時間領域に変換する。
離散時間フーリエ変換の定義式を以下に示す。
離散時間フーリエ逆変換の定義式を以下に示す。
このは正規化角周波数を表す連続変数であり、
は
に含まれる正規化角周波数
の振動成分の量を表す。
また、
は周期
の周期関数で、通常
の範囲で考える。
なお、サンプリング周期をとしたとき、非正規化角周波数
と正規化角周波数
の間に以下の式が成り立つ。
これを線形・時不変システムで図示すると以下の通り。

しかし、計算機で解析するには、無限和の解消と周波数領域の離散化が必要であることがわかる。
離散フーリエ変換|離散時間領域と離散周波数領域
離散フーリエ変換(Discrete Fourier Transform; DFT)は、信号を離散時間領域→離散周波数領域に変換する。 もちろん、離散フーリエ逆変換は、信号を離散周波数領域→離散時間領域に変換する。
離散フーリエ変換の定義式を以下に示す。
離散フーリエ逆変換の定義式を以下に示す。
は離散時間
(整数)で定義された周期
の周期関数であり、
も整数
で定義される周期
の周期関数である。
は周波数のインデックスを表す整数で、
は
に含まれる正規化角周波数
[rad]の振動成分の量を表す。
これを線形・時不変システムで図示すると以下の通り。

なお、畳み込み式は次式で定義される。
高速フーリエ変換(FFT)
結局、周波数解析で求めたいのはまたは
であるが、計算機で解析するために様々な近似を経て、
を計算して解析を行う。
しかし、DFTでも計算時間がであり、現実的ではない。
そこで一般には、この計算時間がになる高速フーリエ変換(Fast Fourier Transform; FFT)を利用する。
このFFTでは、そのアルゴリズムや計算機の性質からなど2の乗数の点数で計算を行うと高速にできる。
アルゴリズムの詳細はここでは議論しない。
フーリエ変換のまとめ
ここまで3種のフーリエ変換について概要を述べたが、これらにフーリエ級数展開を加えて、離散性と周期性に注目して以下に整理する。

なお、フーリエ級数の定義式を以下に示す。ただし、ここでは議論しない。
実装時のポイント
Pythonの信号処理ライブラリで有名なSciPyを使う場合、主に以下の2つの関数を使います。
- scipy.fftpack.fft
中身はDFTのFFTです。戻り値はですので、複素数であることに注意しましょう。
また、一般に周波数解析でy軸にとるのはなので、適宜パワースペクトルに変換します。
- scipy.fftpack.fftfreq
scipy.fftpack.fftの戻り値に対応する、離散化された周波数を計算する関数です。
必要に応じて正規化各周波数→非正規化角周波数に変換します。
NumPyにも numpy.fft.fftとnumpy.fft.fftfreqという同じ関数が用意されていますが、SciPyの方が速度が速いそうです。
付録|複素数 オイラーの公式
複素数の理解のため、オイラーの公式を下記に示す。
なお、オイラーの等式は以下の通り2。
詳細は下記を参照のこと。
おわりに
数学的な議論や定義式の導出は省き、要点だけをまとめました。
(大変だった。。。)
これを見れば、なぜFFTの戻り値が複素数なのか、なぜfreqの計算結果がから
の値なのかがわかると思います。
参考になれば幸いです(^^)
(追記)
周波数解析のPython実装例はこちらの記事にありますので、よろしければご覧ください。
ディジタル信号処理|周波数解析とFFT(実践) - ari23の研究ノート
参考文献
参考文献は以下の通りです。
リンク
技術書