データ同化(またはベイジアンフィルタ)の1つであるカルマンフィルタと尤度について、自分なりの理解をまとめます🐜
この記事を書くにあたり色々調査したところ、素晴らしい記事がたくさんありますので、それをうまく参照しながら整理します。
カルマンフィルタの難しさ
カルマンフィルタはよく使われる技術ではあるんですが、理解がすごく難しいなぁと思っています。 というのも、例えばカルマンフィルタを解説する技術書や記事を見ても、その目的が制御なのか推定なのか、次元が一次元なのか多次元なのか、などで書きぶりがかなり変わってくるように感じています。
特に制御理論で発展した技術なので、著者が制御の人間かどうかで解説の仕方もかなり違う印象です。
以降でカルマンフィルタを解説しますが、このブログでは『データ同化入門-次世代のシミュレーション技術-(朝倉書店)』の内容に軸足を置き、制御理論との間を少しだけ埋めるよう意識します。
線形・ガウス状態空間モデル
以前の記事で、データ同化の基本である状態空間モデルを扱った。
データ同化|データ同化とは ざっくり解説 - ari23の研究ノート
上記の記事では、システムモデルと観測モデルの線形性や、システムノイズや観測ノイズの確率分布に言及していない。
カルマンフィルタでは、システムノイズと観測モデルは線形モデルであり、システムノイズや観測ノイズはガウス分布(正規分布)に従うとする。つまり、状態空間モデルを以下のように書くことができる。
各変数の説明と形は以下の通り。ただし、※がついた名称は一般的ではない可能性があることに注意されたい。
| 変数 | 次元 | 説明 |
|---|---|---|
| 時刻 |
||
| 時刻 |
||
| 時刻 |
||
| 時刻 |
||
| - | 時刻 |
|
| 時刻 |
||
| 時刻 |
||
| 時刻 |
||
| - | 時刻 |
|
| 時刻 |
分散共分散行列とは、分散の概念を一次元から多次元(多変量)の確率変数に拡張し行列で表現したものである。
以下に、ガウス分布(正規分布)に従う二次元確率変数
の確率密度関数
を示す。
参考として、一次元の確率分布を以下に示す。
制御理論の場合
制御理論、特に現代制御では状態空間モデルを、例えば以下のように表すことが多いと思います(MATLABのカルマンフィルターを参考)。
変数の違いはもちろんですが、一番の違いは入力のです。私は制御もかじっているせいか、この
によってかなり混乱しました。しかし本質はまったく同じで、この入力を状態変数
に入れてしまえば、最初に出した状態空間モデルと一致します。
予測とフィルタ
カルマンフィルタのアルゴリズムに入る前に、予測とフィルタ(濾波ともいう)の考えを導入する。
データ同化は、モデルと観測値をうまく馴染ませる技術であると説明した。
データ同化|データ同化とは ざっくり解説 - ari23の研究ノート
今、時刻において、状態変数
を予測することを考えたい。
このとき、手元には時刻から
までの(時刻
以外の)観測値があり、これを
と書くことにする。
の確率(密度)は、
を条件とする、条件確率として以下のように書ける。
これを予測分布と呼ぶ。
次に、同じく時刻のときに観測値
が追加されたとする。新たに情報が追加され、
の条件確率が更新される。
これをフィルタ分布と呼ぶ。
カルマンフィルタをはじめとする、逐次ベイズフィルタでは、この(一期先)予測ステップとフィルタステップ(更新ステップともいう)を交互に操作して分布を求める。以下は、この予測とフィルタを図示したものである。
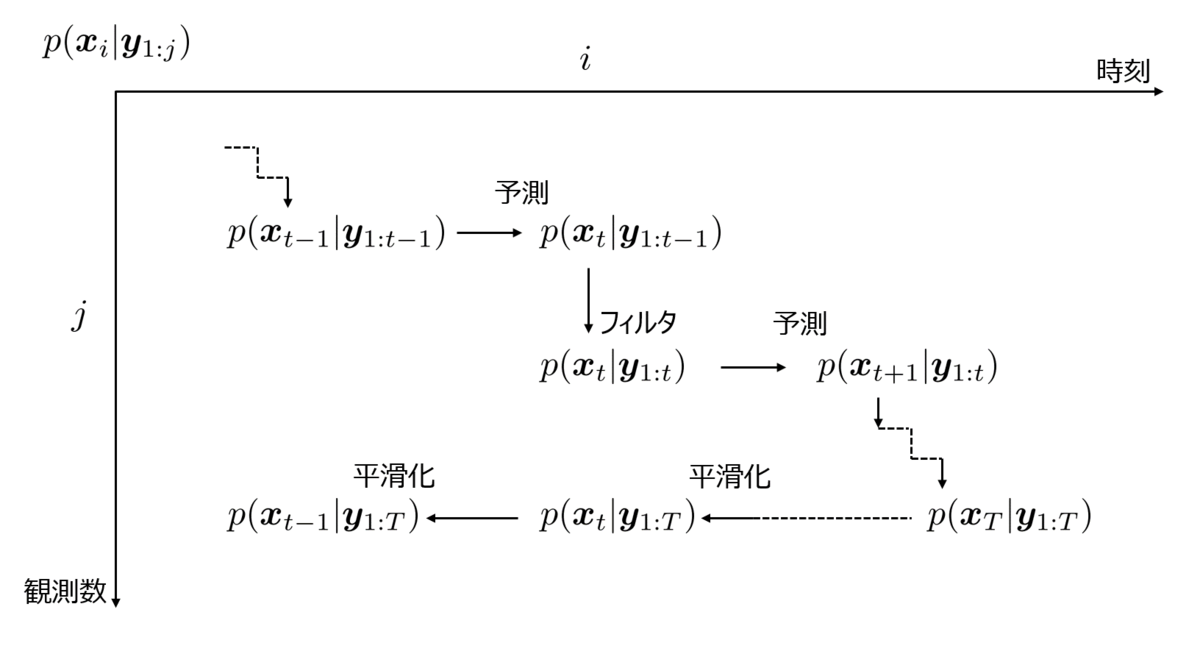
ここでの「分布を求める」とは、各ステップでのガウス分布の平均と分散共分散行列を求めることを意味する。つまり、推定値はフィルタステップで得た平均値である。
また、フィルタステップでは観測値が追加され、より真値に近い分布に更新されるので、分散がその分だけ小さくなるイメージを持てば良い。
ところで、以下の分布は全区間での観測値を使って求める時刻での分布であり、これを平滑化分布と呼ぶが、ここでは扱わない。
以上を次の表でまとめる。
| 分布名 | 表記 | 観測値の区間 |
|---|---|---|
| 予測分布 | |
1ステップ前まで |
| フィルタ分布 | |
今のステップまで |
| 平滑化分布 | |
全区間 |
カルマンフィルタ
カルマンフィルタのアルゴリズムは次の通り。なお、は
の転置行列を表す。参考として、線形・ガウス状態空間モデルも再掲する。
線形・ガウス状態空間モデル(再掲)
カルマンフィルタアルゴリズム
<初期条件>
を初期の状態変数、
を初期の状態変数の分散共分散行列とし、時刻
に対して、次の操作を行う。
<一期先予測>
<フィルタ>
各変数の説明は以下の通り。
| 変数 | 説明 |
|---|---|
| 時刻 |
|
| 時刻 |
|
| 時刻 |
|
| 観測残差の分散共分散行列 | |
| 最適カルマンゲイン | |
| 観測値が追加され更新した時刻 |
|
| 観測値が追加され更新した時刻 |
カルマンフィルタでは原則、この一期先予測とフィルタの操作を交互に繰り返して、状態変数の平均ベクトルと分散共分散行列を求めながら、真値に近い値を推定する。その様子を図示したものは以下の通り。

例えば、時刻での予測分布は
であり、フィルタ分布は
であることを示す。
アルゴリズムの導出
カルマンフィルタのアルゴリズムとその導出については、以下の記事を参考にされたい1。
シンプルなモデルとイラストでカルマンフィルタを直観的に理解してみる
カルマンフィルタのイメージを図で丁寧に書かれていて、感動しました。
特に一次元と多次元で比較した表が非常にわかりやすいです。時系列解析(8)-状態空間モデル-
時系列解析において多くの書籍を出している北川源四郎先生の講義資料です。
式の導出も書かれています。カルマンフィルタの基本式:カルマンフィルタでロボットの位置推定をしてみよう(2)
カルマンフィルタの操作で求める各変数を丁寧な解説してあります。
尤度
カルマンフィルタなどデータ同化を扱うときに最も難しいのは、真値がわからない状態でノイズなどのパラメタを設定することである。このとき、パラメタ設定の指標として尤度を使うのが一般的である。
尤度とは全区間の観測値の同時確率であり、と表現できる。これを乗法定理
を使うと、以下のように書き下せる。
は、時刻
の観測値に対して、最初から1ステップ前の過去の観測値
をもとに予測したときの実際の観測値
の確率である。(一期先予測尤度ともいう。)
このについて、予測分布から考えてみたい。
時刻の予測分布は
であり、線形・ガウス状態空間モデルであれば平均ベクトルが
で、分散共分散行列が
であるガウス分布に従う。
次に観測モデルを通すと、
は平均ベクトルが
で、分散共分散行列が
であるガウス分布に従うとわかる。
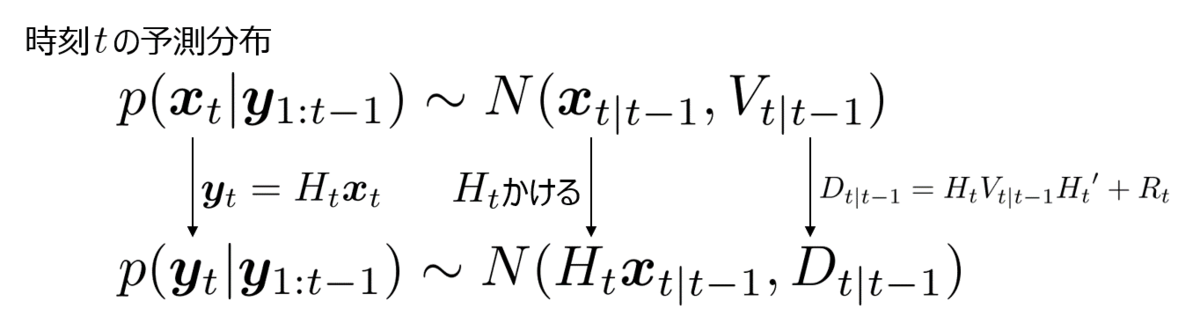
つまり、は以下のように書ける。
と
の違いに注意すること。
ところで、もしにパラメタベクトル
(例えばシステムノイズなど)が含まれる場合は、
は
の関数とみなせるので、
と書いて、これを尤度関数
と呼ぶ。
整理すると以下の通り。
ただし、尤度関数は非常に小さい値であるため、ハイスペックな計算機でもアンダフローを起こしてしまう。そこで、尤度関数に対数を導入した対数尤度関数
を求めることで、アンダフローを回避するのが一般的である。
ここで、だけに注目する。
改めてに戻ると、以下のように書ける。
結局、尤度を計算するのは難しいため、この対数尤度関数の値を指標とする。多くの組み合わせの中から、対数尤度関数の値が最大となるパラメタを、最も確からしいとして採用する。この対数尤度関数を単に尤度と呼ぶこともあるので注意する。
なお、このように尤度を比較する場合、の最終結果にある係数
は本質的に意味をなさないため、アンダフローを回避する目的で省略することもある。
おわりに
データ同化の代表技術の1つである、カルマンフィルタについて整理しました。 特に参考書などで省略されがちな尤度の式展開をとても丁寧に書いてみました。(これが一番大変でしたw)
本記事と、途中でご紹介した素晴らしいリンクを見比べながら、読み進めていただくと理解しやすいと思います。
参考になれば幸いです(^^)
なお、放物線投げ上げをカルマンフィルタで予測する例は以下の通りです。これらもぜひご覧ください。
データ同化|カルマンフィルタと斜方投射への適用例 - ari23の研究ノート
データ同化|斜方投射のカルマンフィルタをPythonで実装 - ari23の研究ノート
参考文献
参考文献は以下の通りです。
データ同化入門 (予測と発見の科学)
データ同化分野で私にとってのバイブルです。決して簡単ではないですが、数学的議論がかなりきちんとなされています。データ同化に取り組むときは、まずこれを読んでいます。カルマンフィルタの基礎
工学の視点からカルマンフィルタが丁寧に説明されています。カルマンフィルタならこれがおすすめです。時系列解析の方法 (統計科学選書)
カルマンフィルタはもちろん、タイトル通り時系列解析の手法が解説されています。比較的読みやすいです。
-
紹介した記事がとても素晴らしいため、自分で書くのはやめて、その分各変数の説明を丁寧に書きました。↩